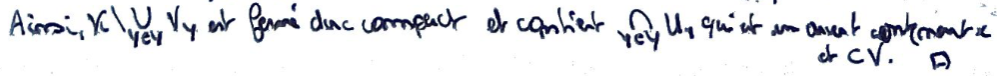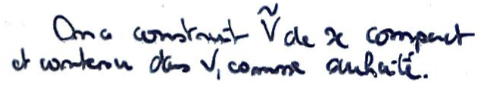Montrer que si tout point admet un voisinage compact, alors tout point admet une base de voisinages compacts.

Pour un point quelconque, on prend un voisinage compact et un voisinage ouvert arbitraire.

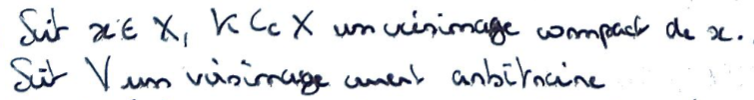
On utilise la séparation du voisinage compact pour prendre des ouverts disjoint avec les autres points du voisinage compact.

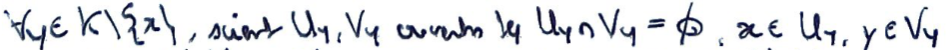
Ajouté au voisinage ouvert, cela donne un recouvrement, dont on peut extraire un sous-recouvrement fini.

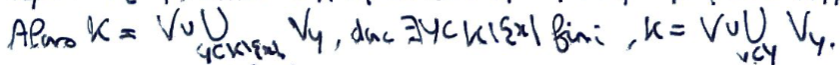
Retirer ce recouvrement donne un voisinage fermé (donc compact) de \(x\) contenu dans le voisinage ouvert initial, donc c'est gagné.